PARA VER INGRESOS ANTERIORES

PARA VER LOS PUBLICACIONES  ANTERIORES
HAZ CLIC AQUI:

ENTRADAS ANTIGUAS

El ariete hidráulico

MOTOBOMBA ECOLOGICO

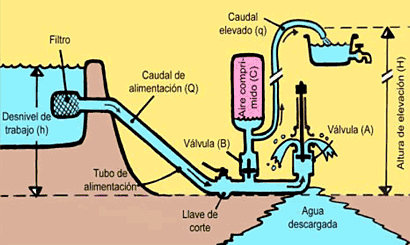
El ariete hidráulico, patentado en 1796 por Joseph Montgolfier, consiste en una máquina que aprovecha únicamente la energía de un pequeño salto de agua para elevar parte de su caudal a una altura superior. A partir de su invención, el ariete hidráulico tuvo una amplia difusión por todo el mundo. Baste decir, a modo de ejemplo, que estuvo presente en las famosas fuentes del Taj Mahal en la India, o en el Ameer de Afganistán. Con el tiempo cayó en desuso, sobre todo debido al avance arrollador de la bomba centrífuga. En la actualidad asistimos a un renacer del interés acerca de este aparato, debido a que es tecnológicamente accesible, eficiente, y ecológico, ya que funciona sin necesidad de alimentación energética.

VIDEOS INFORMATIVOS

INVESTIGA

1. RESEÑA HISTORICA DE ARIETE HIDRAULICO
2. FUNDAMENTE FISICO-MATEMATICO DE ARIETE HIDRAULICO
3. EL USO Y SU IMPORTANCIA EN LA AGRICULTURA
4. DISEÑE UN ARIETE HIDRAULICO

VISITE LA PAGINAS

1. http://news.soliclima.com/divulgacion/eficiencia-energetica/fabriquelo-usted-mismo-el-ariete-hidraulico

TEODOLITO CASERO

APLICANDO LA TRIGONOMETRIA

Los babilonios y los egipcios (hace más de 3000 años) fueron los primeros en utilizar los ángulos de un triángulo y las razones trigonométricas para efectuar medidas en agricultura y para la construcción de pirámides. También se desarrolló a partir de los primeros esfuerzos hechos para avanzar en el estudio de la astronomía mediante la predicción de las rutas y posiciones de los cuerpos celestes y para mejorar la exactitud en la navegación y en el cálculo del tiempo y los calendarios. En este capitulo, se construirá un instrumento para hacer diferentes mediciones usando  conceptos básicos de la trigonometría. VIDEO DE CONSTRUCCION DE UN TEODOLITO CASERO PREGUNTAS PARA INVESTIGAR Analiza la evolucion historica de la trigonometria ¿Cuales son las herramientas andinas (etnoandinas) para la medicion de la tierra? Diseñe un teodolito sencillo usando materiales del medio VISITE PAGINAS WEB http://www.dav.sceu.frba.utn.edu.ar/homovidens/Loponte/ProyFinalLoponte/proyectofinal/historia.htm  http://www.youtube.com/watch?v=zLuMq1AeW4U http://www.cienciafacil.com/TeodolitoSimple.html

HOGAR ECOLOGICA

Reducir el impacto ambiental de nuestras acciones diarias, contribuirá a mejorar la calidad de vida en el planeta. Para ello hemos de intentar: RECUPERAR, RESPETAR, REDUCIR, REUTILIZAR Y RECICLAR.

TAREA:

Defina cada una de los términos: Recuperar, respetar, reducir, reutilizar y reciclar.

Visite a las paginas de link. e investigue mas sobre hogar ecologico y dibuje o diseñe una maqueta de un hogar ecologico.

VISITE LAS PAGINAS:

http://www.ecoaltea.org/hogar-ecologico/hogar-ecologico/

http://www.youtube.com/watch?feature=endscreen&v=_DVjFGVSHi4&NR=1

http://www.youtube.com/watch?feature=endscreen&NR=1&v=sWXUmenIKfU

VIDEOS

LA CHICHA DE JORA: BEBIDA ENERGIZANTE

LA CHICHA DE JORA

  La chicha de jora. Es una bebida nutritiva y sabrosa, heredada de la cultura incaica la cual era considerada sagrada, bebida tradicional que se consume en los sectores medios y populares, utilizada como ingrediente para sazonar variadas recetas del norte y centro del Perú.

PREGUNTAS PARA INVESTIGACIÓN:

¿Que propiedades tiene la chicha de jora  no fermentada?
¿Que propiedades tiene la chicha de jora  fermentada?
¿Podemos incluir la chicha en la dieta diaria?

VISITA LA SIGUIENTES PAGINAS
http://wiki.sumaqperu.com/es/Chicha_de_jora
http://www.ecured.cu/index.php/Chicha_de_jora
http://historiagastronomia.blogia.com/temas/14-la-chicha.php

USO DE SOFTWARE COMO RECURSO DIDACTICO

Software de aprendizaje colaborativo SMART Notebook

Haga del aula un lugar más interactivo y atraiga la atención de sus alumnos con el software SMART Notebook.Con unas potentes herramientas para diseñar e impartir clases, complementos funcionales y una edición aparte para alumnos, creará momentos de aprendizaje extraordinarios de forma fácil.

AQUI MANUAL DE USO BASICO

VIDEO DE PRESENTACION DE SMART NOTEBOOK

DESCARGAR SMART NOTEBOOK (VERSION DEMO)

VIDEO MUESTRA INSTALACION DE SMART NOTEBOOK

DE INTERES

BASES PARA CONCURSO FENCYT 2012 APROBADAS POR EL MINISTERIO DE EDUCACION

DIRECTIVA 027 APROBADA POR LA UGEL HUAMANGA: BASES PARA CORCURSO DE FENCYT 2012 AMBITO UGEL HUAMANGA

ROTAFOLIO COMO RECURSO DIDACTICO

 Descripción del rotafolio

Es una herramienta pedagógica de carácter visual que sirve de apoyo a las y los docentes que desarrollan sesiones.El rotafolio está conformado por un conjunto de láminas de papel, tela u otro material en que se plasman ideas, mensajes o información apoyándose en imágenes y gráficos, siguiendo una secuencia lógica y ordenada que permite la fácil comprensión del tema.
El rotafolio como recurso didáctico

View more presentations from Desirée Jiménez

DEMOSTRACION DE LOS VOLUMENES

VIDEO 1:

VIDEO 2:

DEMOSTRACION DEL VOLUMEN DE UNA ESFERA

DEMOSTRACIÓN DEL VOLUMEN DE ESFERA

Como todo el mundo sabe (o debería saber ya que se estudia en el colegio) el volumen de una esfera de radio R es:

Esta fórmula se debe al genial Arquímedes, y fue uno de sus grandes descubrimientos y del cual estaba muy orgulloso. Vamos a ver cómo lo consiguió.

Arquímedes partió de una semiesfera de radio R y colocó a su lado un cono recto y un cilindro circular recto, ambos con base de radrio también R:

Cortó las tres figuras con un plano paralelo a la base del cilindro (que quedara a distancia dde la parte superior de las tres figuras) y estudió cómo serían las secciones que este plano crearía en cada una de las figuras:

• Cilindro: circunferencia de radio R.
• Semiesfera: también una circunferencia pero de distinto radio, digamos r. Mirando la siguiente figura
  
  y usando el teorema de Pitágoras tenemos que r²+d²=R².
• Cono: también una circunferencia, pero ahora, como podemos se ve aquí
  
  el radio es d.

Por tanto tenemos:

Sección cilindro=πR²=π(r²+d²)=πr²+πd²=Sección semiesfera+Sección cono

Las secciones de cada figura son como rebanadas de las figuras:

Si para cada rebanada se tiene la relación anterior parace bastante claro que los volúmenes siguen la misma relación. Es decir:

Volumen cilindro=Volumen semiesfera+Volumen cono

Pero Arquímedes conocía los volúmenes del cilindro y del cono:

Por tanto:

De donde multiplicando por 2 obtenemos el volumen de una esfera de radio R:

Tanto admiraba Arquímedes este descubrimiento que mandó inscribir en su tumba la siguiente imagen:

VIDEO DEL VOLUMEN DE ESFERA

GUIAS DIDACTICAS

“La matemática tiene las progresiones geométricas que elevan los números  a maravillosa altura, las sociedades tienen la educación”.

                                                                                                                       José Martí

MATERIALES DIDACTICOS:

SILABOS DE MATEMATICAS

Guia didactica de circunferencia.

 Guia didactica de relaciones metricas en un triangulo.

Guia didactica de areas de regiones planas.

Guia didactica de geometria de espacio 1.

Guia didactica de geometria de espacio 2.

Guia didactica de introduccion a programacion lineal.
Guia didactica de funciones exponenciales y logaritmicas.
Guia didactica de analisis combinatorio.
Guia didactica de angulo trigonométrico.
Guia didactica de razones trigonometicas en un triangulo rectangulo.
Guia didactica de angulo en posicion normal y circunferencia trigonometrica.
Guia didactica de identidades trigonometricas.
Guia didactica de Funciones trigonométricas.
EXAMEN